The geodetic latitude is given by the angle between the normal to the spheroid and the plane of the equator. The normal to the spheroid is the normal to the tangent plane of the spheroid. Let r be a point on the surface of the spheroid. Then the tangent plane at r is given by ...
Where s and t are the unit vectors along s and t at r.
The normal is perpendicular to all vectors in the tangent plane.
Thus the normal is ...
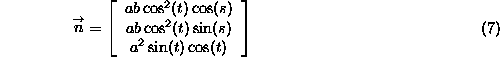
The projection of the normal onto the equatorial plane is given by
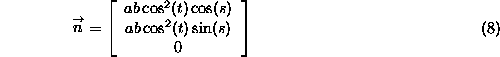
The cos of the angle between the normal and the equatorial plane is given by the dot
product of the normal vector and its projection divided by their lengths.
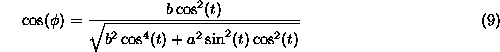
Multiply by cos2(t)/cos2(t)...
This implies that 
is
the angle in a right angled triangle with adjacent side b and hypotenuse 
and opposite side, (by
pythagoras), of a 
.
Thus the 
would be the
opposite side over the adjacent side, giving as...
Solving the definition of e for b gives us...
Thus...
