as a power series.To express t as a function of 
we can just invert both sides of the
differential equation defining and use it to calculate the terms of the
Taylor expansion of t in terms of .
To make this easier, first perform a change of variable 
. Then
Then the defining equation becomes...
Then we can calculate higher derivatives like so...
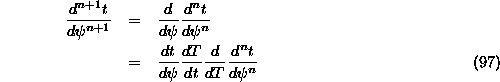
As T=1 when 
, calculate the derivatives of t with respect to and set T=1 and
place them into the Taylor series. In this equation I have neglected terms in 
and
higher...
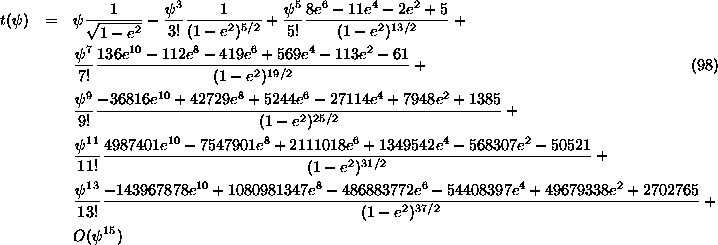
I would not recommend this approach except at very low latitudes, as it converges too slowly.