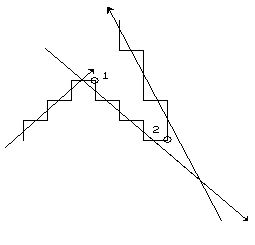
Figure 14Link point1 is in the
"Future", Link point2 is
"ElseWhen"
As they are found, the lines are placed in a container. After all lines have been found, the first and the last vexils are thrown in at the front and the back of the container. These provide 'ties' to the node points. The container is then scanned, and the start point, every intersection point between successive lines, and the end point is output to disk.
The exactness constraints guarantee that lines are exact as far as the string goes. If the line projects beyond the end of both strings before it intersects the next line, then exactness is not guaranteed.
To handle this problem a simple test is needed to identify such cases.

Figure 14Link point1 is in the "Future", Link point2 is "ElseWhen" |

Figure 15. Previous example after smoothing. |
The link-point is the point which joins the two strings being approximated.
The join-point is the point where the two approximating lines intersect. (Normally this point would be output from the program).
Make an affine transformation of the coordinate system to a new non-orthogonal coordinate system which has the join-point as its origin and the two approximating lines as its axes.
Calculate the coordinates of the link-point in the new coordinate system. If the link-point is in quadrant 2 or 4 of the new coordinate system then it is else when, and the lines extend beyond the end of both strings.
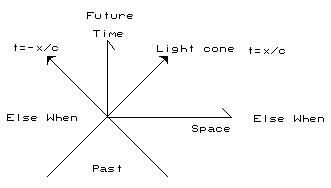
Figure 16. Spacetime diagram illustrating the concept of "Else When". |
Past :- Those points in space-time that could causally affect a particle at the origin.
Future :- Those points in space-time that could be causally affected by a particle at the origin.
Else When :- Those points of space-time that cannot causally affect or be affected by a particle at the origin.
The exactness constraint can only be violated in the "Else When" case, but to actually calculate when the exactness constraint is violated is tedious in the extreme, but does not pose any technical or computational difficulties.
If the link-point is Else When then the following algorithm is used :-
If exactness is not violated Then
output the join point
Else
If the join point is closer to the first vexil of the second
string than the last vexil of the first string Then
output the intersection of the first line and the last vexil
of the first string.
output the intersection of the second line and the last vexil
of the first string.
Else
output the intersection second line and the first vexil
of the second string.
output the intersection of the first line and the first vexil
of the second string.
As an extreme case of Else When, the two lines may in fact be parallel, thus there is no join point. In this event, the lines an either be parallel or anti-parallel.
Figure 17. Anti parallel lines. |
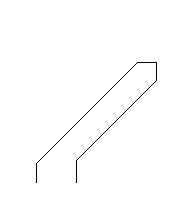
Figure 18.Result of linking algorithm. |
If as in Figure 17, the lines are anti-parallel then the two lines are joined via three points. The intersection of the first line with the last vexil of its corresponding string, the link-point that joined the original two strings, and the intersection of the first vexil of the second string with its corresponding line. The link-point is added to prevent too much of the pixel on the end being cut off.

Figure 19. String Resulting in two parallel lines. |

Figure 20.Result of algorithm. |
If as in Figure 19, the lines are parallel, then the link-point
joining the two original strings is not added as the intermediate
pixel is safe in this case.
| Previous | Next | Contents |