To calculate L(t) from (55) is very easy with an
algebraic manipulation package, simply let 
and compute the Taylor series expansion of
with respect to g and
then integrate with respect to t and multiply by a. Let S = sin(t) and C = cos( t) then
the result is..
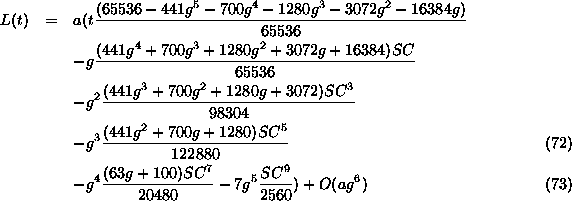
Another curiosity of the changes in our computation methods is that the original papers give this expansion in terms of sin(2t), sin(4t), sin(6t) etc. In those days multiplications such as needed to calculate the powers of cos(t) where performed by using a table lookup to get the logs, summing and then again using tables to take the anti-logs. This results in a computation time disadvantage in expressing it in powers of cos(t). For the modern computer, the old approach would required 5 very expensive in clock cycles sin calculations instead of only 1 cos and 1 sin and about 7 relatively cheap floating point multiplies. On a 80486 a floating point multiply takes 16 clock cycles and a sin takes about 241 clock cycles.
.