The cos of u, the angle between these two displacements can be calculated from the
scalar product...
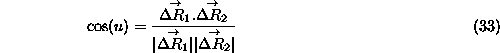
Now by the conform property we can equate the 
calculated on the map and
on the surface of the earth. Thus :-
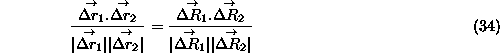
Thus putting all the details in we get...
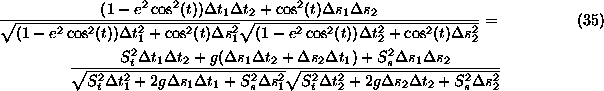
Now as the delta's are small but arbitrary we can set ...
Then equation (37) becomes...
Which implies that g=0. Using the definition of g in equation (32) we get the partial differential equation...
This simplifies equation (37) to ...
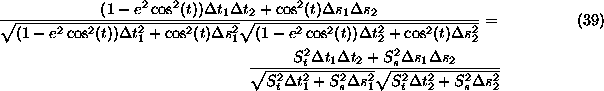
As the delta's are small but arbitrary we can set 
then the above becomes...
Squaring both sides and simplifying gives you...
Which as the terms in 
cancel...
Now one can use the result of g=0 to relate 
and 
...
Thus solving this for ...
And using it to remove from equation 43...
We can cancel on either side and simplify...
Now take square roots of both sides....
Plugging this into the equation (39) resulting from g=0
gives us...
We wish to define a map projection whose axis orientation matches standard mathematical practice, and more particularly, matches the ARC/INFO GIS, Y increases with latitude and X increases with longitude eastwards. Thus we choose the sign in (49) to be +ive and the sign in (48) to be -ive.