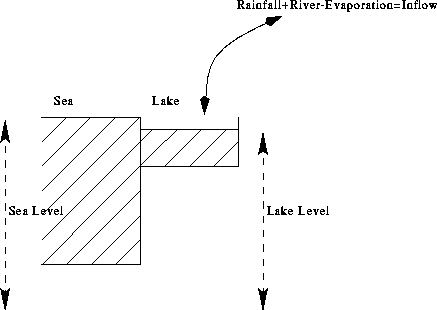
Figure 15: Single lake cell the level dependent estuary and time dependent inflow
If we have a constant river+rainfall+evaporation inflow, one square sided cell and a linearly level dependent estuary, (See figure 15)

Figure 15: Single lake cell the level dependent estuary and time
dependent inflow
![]()
Opening or closing Potter's channel would correspond to changing the value of k.
Rearranging slightly so we may more easily see the homogeneous part.
![]()
Then the solution is...
![]()
Note one small detail. ![]() is not the volume of water in the cell
at time t=0.
is not the volume of water in the cell
at time t=0. ![]() is merely a constant of integration. Now for interests sake let us
put this in terms of
is merely a constant of integration. Now for interests sake let us
put this in terms of ![]() , the volume of water at time t=0.
, the volume of water at time t=0.
![]()
Which implies...
![]()
So the equation (51) for the volume becomes...
Volume as a function of time.
A pair of terms of the form ![]() is the mathematics way of taking the system from
the initial condition A at time t=0 to the final condition B at time
is the mathematics way of taking the system from
the initial condition A at time t=0 to the final condition B at time ![]() .
.
The final steady state condition ![]() is made up of two terms...
is made up of two terms...
Denote the salt load by S. Now the load calculation, assuming no salt in the inflow, is...
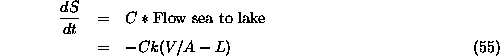
Where C is the salt concentration of sea water (![]() ) when V/A
> L and is S/V when the flow is from lake to sea.
) when V/A
> L and is S/V when the flow is from lake to sea.