Suppose the lake is in a hyper-saline situation with a near maximal head difference
between the lake and the sea. Then any compensation releases would simply be absorbed by
the lake without changing the direction of the sea to lake flow. In this case we can
calculate the amount of salt prevented from entering the system by a release of volume ![]() .
.
In this case we have Sea to Lake flow. Unfortunately we cannot assume we are operating beyond the effect of any transients, as the sudden release of water creates a transient, followed by another transient when the release ceases.
The full salt load equation from (60) is...
![]()
Now there are three phases in this problem...
So at time t=0, V(0) = A(I/k+L), and ![]() .
.
At time ![]() ,
,
![]()
Now we can calculate the load at a time after the release has finished...
![]()
We need the volume at time ![]() from equation (54)...
from equation (54)...
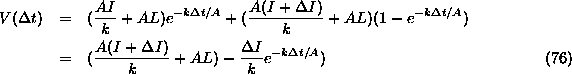
Substituting for the known values at time ![]() ...
...
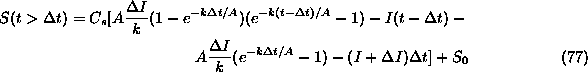
Now we wish to know the full effect of the release, so for t large enough...
![]()
Comparing this with what the load would have been without a release we have...
![]()
Which is interesting in both its simplicity, and the total lack of effect of the transients.