What is the Gauss conform system?

Firstly the caveat should be issued that while the numbers are crudely approximated by the Transverse Cylindrical Projection, the Gauss Conform projection does not in any way arise from wrapping cylinders around globes.

The Gauss Conform projection arises from placing a set of mathematical constraints on the set of all projections. The constraints are sufficient to uniquely determine the projection.

The heart of the trick lies in the word ``conform'', which means that locally, angles measured on the surface of the earth are preserved across the projection. This constraint implies, (after a fair patch of algebra), a pair of coupled partial differential equations. The other constraints are boundary conditions on the pde's.

In the definition of conform the word ``locally'' arises. This means the property of being angle preserving holds only over distances very small compare with the radius of curvature.

What should the average Joe Blogg's of Remote Sensing and GIS know about this projection?

• The Gauss Conform projection is used on all South African 1:50000, 1:10000 and 1:250000 scale maps and images.
• It is a conform projection. Hence, over distances small compared with the radius of the earth, the shape of things on the earth is exactly the same as the map.
• There is a scale distortion that increases from zero as you go away from the central meridian. Ie. If points A and B are far from the central meridian, and you walk from A to B and find the distance to be X kilometers. Then you will find that the distance as shown by the map WON'T be exactly X kilometers.
• There is an area distortion. If you measure the area of a region on the ground and on a map you will find they won't be exactly the same.
• If however, you work, (as do all South African maps), within 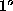of longitude of the central meridian, these errors will be less than 1 part in 6000. However if you patch a large number of images together all on the same central meridian, these errors will grow.
• South African X axis lies along the central meridian, pointing South. Along the central meridian it has the value of the number of meters of arc South of the equator.
• The central meridian is the ONLY line of longitude that is a straight line on the map.
• The equator is the ONLY line of latitude that is a straight line on the map.
• All lines of latitude and longitude on the earth intersect at right angles. Thus by the conform property all lines of latitude and longitude intersect at right angles on the map.
• The South African maps make use of the geodetic latitude, this means you MUST specify the Modified Clarke 1880 spheroid when you use latitude/longitude coordinates on a computer system.
• Check that your GPS is using the Modified Clarke 1880 spheroid in its internal calculations. If you have existing measurements using the wrong spheroid you must convert them first.
• Most straight lines on the surface of the earth become curved lines when projected. However, unless you densify your arcs first, straight lines remain straight lines when projected by a GIS. A GIS only transforms the end points of an arc and hopes that the error it is making in between is not too large.
• South Africa is changing its map system from the older slightly inaccurate Clarke 1880 spheroid to the WGS84 spheroid. You should note that...
  • The constants of the spheroid ie. The semi-major radius and semi-major radius are different.
  • The origin of the (x,y,z) coordinate system is being shifted. So it is NOT sufficent when changing to the new system to convert from map coordinates to (x,y,z) and back using the new constants. You must convert from map coordinates to (x,y,z), shift the origin, and convert back using the new constants.
  • Maps use the geodetic latitude, that is the angle between the normal to the spheroid and the equatorial plane. Thus even data that is geographic coordinates, (latitude and longitude), must be converted to the new datum.
  • Whilst it is possible to approximate the change knowing just the latitude and longitude position, to get accurate results you need to know the height of each point as well.
  • There does exist a direct conversion formula that takes you from map coordinates plus height to the new map coordinates and the new height. See [Merry & Rens] for details.