Which latitude?

Latitude comes in at least four non-equivalent flavours...

• Geodetic latitude. This is the angle between the normal to the surface of the ellipsoid and the equatorial plane. This variety is also called Geographic latitude and is used on maps. However it is a right pain to calculate with, but came into use because it is closer to the astronomical latitude which people can measure with a sextant. I will denote it by .
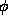• Astronomical latitude. This is the angle between a plumb line and the equatorial plane. Although [Schrieber 1943] implies that Geodetic latitude is Astronomical latitude, there may be up to a minute of arc difference between the two [Bowditch 1958].
• Geocentric latitude. The angle between a line joining the point on the surface of the earth and the center of the earth, and the equatorial plane. I will denote it be t and use it in most of the subsequent calculations.
• Conformal latitude. The Gauss Conform transformation function is not analytic when expressed in terms of any of the above latitudes, but is when expressed in terms of the conformal latitude .

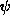I will prove the following later, but just for handy summary purposes...

To transform from geocentric to geodetic...

and from geocentric to conformal...

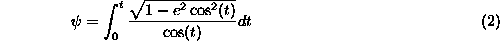
Where a is the semi-major radius of the earth, b is the semi-minor radius and e is the eccentricity. See the section on the constants of the spheroid for more details.