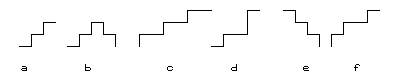
Figure 6. Examples of strings.
The output of most raster to vector conversion routines are strings of vexils outlining the pixels. Unfortunately the corners of the pixels create jagged edges to lines that are not horizontal or vertical. (See Figure 4 for example.) These jagged artifacts are unwanted for two reasons,
Why do we not simply recover the original picture? The rasterizing process loses information, thus there is not sufficient information within the raster picture to recover the original picture. The best we can get is an approximation.
Vectorization is thus an underdetermined problem. The raster image only provides constraints on which vector images are possible.
It would be reasonable to expect the result of a vectorization procedure to have the property that if the polygons were rasterized using the same grid as the original image, exactly the same pixels would result. I define vectorization procedures which have this property as being exact.
However, it should be noted that the requirement that vectorization must be exact does not determine the result.
It turns out that the boundaries of the edge pixels of each region contain all the information on the exactness constraint. So the first step is to outline the boundary pixels of each region.
This step is performed by "The Spaghetti Machine" described earlier. As each string of vexils is completed it is handed over to be smoothed. These strings of vexils are the boundary vectors of pixels so can only run north, south, east or west.
How can one find the least number of vectors to replace this list of vexils? The easiest way is as follows :-
Note that in step 4) any exact line can be output. This is the point where the algorithm is only near-optimal not optimal. It is locally optimal, but to be globally optimal the choice of exact line to use would be influenced by the requirements of other lines. More on this aspect later.
So the second step is to parse these lists of "vexils" into possible lines. For example a string of vexils going north, east, north, east, south, east, cannot possibly be part of a straight line. The parsing is performed by a finite automaton that recognises longest possible lines. The possible lines are then checked for exactness, and a string of the longest possible exact lines is output.
The input to the smoothing algorithm is a list of vexils. Each vexil is essentially a direction, (one of north, south, east or west), and a positive integer distance, (1 pixel, 2 pixels, 3 pixels,...). Through some strings of vexils it is possible to plot an "exact" line and through other strings it is not.
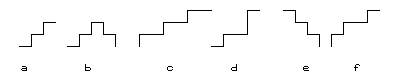
Figure 6. Examples of strings. |
Figure 7.
|
For the purposes of parsing the string of vexils into possible lines, it is convenient to convert the string of vexils into a string of characters. As each vexil can only go in one of four directions, and vexils of length one are very common and important, each vexil is mapped onto the character set {'n', 'e', 's', 'w', 'N', 'E', 'S', 'W'}. Where a vexil of length one will be represented by a lowercase character, {'n', 'e', 's', 'w'} and a vexil of length two or greater will be represented by an uppercase {'N', 'E', 'S', 'W'}.
Thus for example, the string in Figure 7b can be converted into the string of characters "enEnenenEnen".
Of course this translation depends on which way down the string we travel, travelling the opposite way along Figure 7b gives us "swsWswswsWsw".
The process of converting strings of vexils into strings of characters has converted the problem of recognising lines into recognising a formal language.
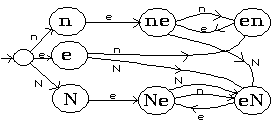
Figure 8. A Finite Automaton to recognise the language ne U nne. |
The language of lines can expressed as a Regular Expression. The definition of a Regular Expression (RE) is :-
It can be shown [Hopcroft & Ullman 1969], that any RE can be recognised by a Finite Automata.
Denote A* U A by A+
The language of simple lines is defined :-
The set of all ne lines ne = {'', 'e'}{'ne'}*{'','n'}
The set of all se lines se = {'', 'e'}{'se'}*{'','s'}
The set of all nw lines nw = {'', 'w'}{'nw'}*{'','n'}
The set of all sw lines sw = {'', 'w'}{'nw'}*{'','s'}
The set of all simple lines is ne U se U nw U sw. Simple lines are easy to handle as all simple strings can be exactly represented by a single line. Only the end two vexils need be considered when calculating the representative line.
The language of complex lines are defined :-
The set of all nne lines = ({'','e'}{'Ne'}+{'','n','N'} U ({'','n','N'}{'eN'}+{'','e'})
The set of all ene lines = ({'','e','E'}{'nE'}+{'','n'} U({'','n'}{'En'}+{'','e','E'})
The set of all nnw lines = ({'', 'w'}{'Nw'}+{'','n','N'} U({'','n','N'}{'wN'}+{'','w'})
The set of all wnw lines = ({'','w','W'}{'nW'}+{'','n'} U({'','n'}{'Wn'}+{'','w','W'})
The set of all sse lines = ({'','e'}{'Se'}+{'','s','S'} U({'','s','S'}{'eS'}+{'','e'})
The set of all ese lines = ({'','e','E'}{'sE'}+{'','s'} U({'','s'}{'Es'}+{'','e','E'})
The set of all ssw lines = ({'', 'w'}{'Sw'}+{'','s','S'} U({'','s','S'}{'wS'}+{'','w'})
The set of all wsw lines = ({'','w','W'}{'sW'}+{'','s'} U({'','s'}{'Ws'}+{'','w','W'})
The set of all complex lines =nne U ene U ese U sse U ssw U wsw U wnw U nnw
Not all complex strings in the complex language can be represented by exactly by a single line. For example the string 'nenenenenEnEnEnEnEnEnEnenenenene' is fairly obviously three strings, a simple ne string followed by a ene string followed by another simple ne string. Thus a more subtle algorithm is needed to find whether a string can be exactly represented by a line. However, the efforts in parsing have not been wasted, as the next algorithm requires other information that only parsing can give it. Furthermore, all simple lines are identified by parsing and thus do not need the computationally more expensive algorithm.
As with many mathematical problems, the problem of finding an exact line is made easier by looking at the dual space.
Consider a line approximating the boundary between two regions of pixels with different classes. Suppose the class on the left of the line is A and on the right B. To be an exact representation, less than 50% of each class B pixel must be on the left of the line and less than 50% of each class A pixel must be on the right of the line.
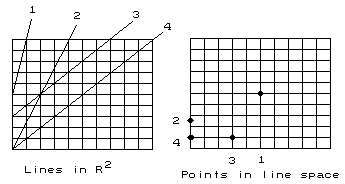
Figure 9. The duality between lines and points. |
Thus the exactness requirement places a set of constraints on which lines are acceptable, ie defines a region within the line space.
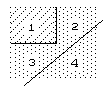
Figure 10. The line must thread the vexils. |
Consider the case in Figure 10, it is clear that there cannot exist a line which does not thread the vexils and is exact. If more than 50% of pixel 2 is below the line, then less than 50% of pixel 3 is below the line, unless the line threads the vexils.
Let the coordinates of the string separating the two regions in Figure 10 be ((1,1), (2,1), (2,2)).
If the line that must represent this boundary is described by the equation y=mx+c, then the constraint that the line threads the vexils can be stated as :-
1 > m*1+c
1 < m*2+c
2 < m*2+c
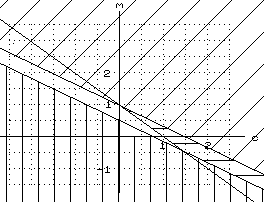
Figure 11.Constraints in line space. |
m < -c + 1
m > -c/2 + 1/2
m < -c/2 + 1
These constraints are illustrated in Figure 11. It should be noted that the feasible region, the unshaded area, is unbounded.
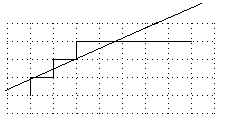
Figure 12.This string cannot be represented exactly by any one line. |
Consider the string, ((1,1), (1,2), (2,2), (2,3), (3,3), (3,4), (8,4)), shown in Figure 12. Clearly the line in Figure 12 threads the vexils, but the last pixel is entirely on the wrong side of the line.
Thus a further constraint is required to guarantee that pixels at the points of vexils are not on the wrong side of the line.
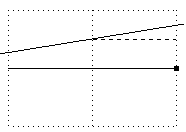
Figure 13. The line must be pinned to the end of the vexil. |
The area of the rectangle below the dashed line is m(x-1)+c-y and the area of the triangle between the line and the dashed line is ½m, thus the constraint is at point (8,4) is :-
7m+c-y+½m < 0.5
The constraints define a feasible region in line space. If the constraints of threading the vexils and pinning the line to the points are applied at every vexil as we scan down the string, then as we scan down the string the feasible region shrinks. If at some point the feasible region disappears, then the string up to but not including the last vexil scanned can be represented exactly by a line. Indeed, any point within the feasible region represents an exact line.
As there are an infinite number of exact lines, we are free to choose. This however is the point at which this program becomes near-optimal, not optimal. An optimal program would choose each line so that the least number of lines would be used. This would require a global knowledge of the string, and considerably more time and effort.
A simple, easy to calculate, but reasonably effective choice is the centroid of the feasible region. As the feasible region is convex, the centroid of the feasible region always lies within the region.
The crux of implementing this smoothing algorithm lies in evaluating and tracking the constraints set up by each vexil in an efficient manner, or this entire approach would become computationally untenable.
All the constraints are linear inequalities. These inequalities thus describe half-planes in line space. For programming purposes a linear inequality may be viewed as a directed line, with the feasible region being on the left of the line. This enables one to use the standard line object.
After two vexils the feasible region is a bounded polygonal region. Thus all that is needed is to maintain a list of the vertices of the polygon.
A region is convex if it is the intersection of half-planes. Clearly the feasible region is convex. This greatly speeds the chopping off of unfeasible vertices. Indeed, if any constraint is introduced that removes the convexity property, (e.g. pinning constraints to improve the optimality), the problem becomes unmanageable.
For two reasons. Simple lines are quite common, and the parsing process is a lot more rapid than evaluating the line space constraints. More importantly, one cannot write down the constraints without information such as the sign of the slope of the line, and whether the line starts above or below the first point in the string. This information is readily obtained from the parser.
Not all lines are worth smoothing. For example, a box is never worth smoothing. Short lines of 4 vexils can be classed easily.
| Previous | Next | Contents |