The hyper-saline events build up over a period of several years. During the summer months of those years, some rain falls, the rivers rise, and some salt is flushed from the system. The problem is that not enough is flushed from the system before the winter dry period starts the salt build up again.
Now assume we made the operating rule that :-
We would make a compensation release of ![]() to flush salt out
of the system.
to flush salt out
of the system.
For convenience define ![]() and
and ![]() . Any quantity with
a prime denotes the same quantity as the unprimed version, but with all I replaced by
. Any quantity with
a prime denotes the same quantity as the unprimed version, but with all I replaced by ![]() .
.
For flow from lake to sea we have...
![]()
At time ![]() we have...
we have...
![]()
Where....
![]()
The load at any time after ![]() is...
is...
![]()
Where...
![]()
Denote the load including the effect of the release by ![]() . Substituting in
for
. Substituting in
for ![]() ...
...
![]()
Which after half a page of algebra simplifies to...
The load after a summer flushing release.
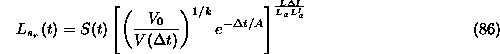
Thus again physically speaking the load is made up of three parts...
Just a small consistency check, if ![]() or
or ![]() is 0, then we get
the same value as the original formula.
is 0, then we get
the same value as the original formula.
Assume the compensation release is small compared to the volume of the lake. Now use
Taylor's theorem to first order to estimate the change in load due to the release.
![]()
Denote the salt concentration in the lake by ![]() .
.
![]()
The last term is a correction factor near 1. In the ``prevent salt influx'' scenario, the
load prevented from entry was ![]() , where as here the amount flushed goes as
, where as here the amount flushed goes as ![]() .
.
Thus if the lake is hyper saline, more is achieved by flushing. Note however, one's efforts are ``watered down'' if the natural inflow continues.