This is a little subtle and apt to confuse. The basic idea is that the derivative of the state vector depends on both time and the value of the state vector at that time.
This places us in a recursive quandary; we need the value of the state vector at time ![]() to
calculate the value of the state vector at time
to
calculate the value of the state vector at time ![]() .
.
What we do is assume that the derivative doesn't change radically in one time step and
use the values at the previous time steps to make a guess of the value at time ![]() .
Then we can resolve our recursive problem by use this predicted value to gain a better
estimate of the state at time
.
Then we can resolve our recursive problem by use this predicted value to gain a better
estimate of the state at time ![]() .
.
So using Taylor's theorem again. This time with ![]() and the predicted
value of the state to calculate the derivatives.
and the predicted
value of the state to calculate the derivatives.
![]()
Where for some ![]() in
in ![]() ...
...
![]()
Now we still lack an estimate of ![]() so we manufacture one using the value of
so we manufacture one using the value of ![]() and
and
![]() .
.
![]()
Where for some ![]() in
in ![]()
![]()
Solving for ![]() we have...
we have...
![]()
Solving for ![]() and inserting the above estimate of
and inserting the above estimate of ![]() we get the
corrector...
we get the
corrector...
Corrector
![]()
Where...
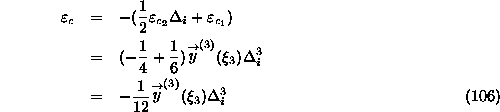
Which is likely to be noticeably smaller than the error for the predictor.
However I suspect that the errors made by the corrector relative to the predictor are even smaller than it would seem on the surface. Why? The corrector takes into account any discontinuous changes in the inputs that may have occurred in the last time step. Indeed these discontinuous changes in the input add weight to the standard arguments for a second ``purifying'' evaluation of the derivatives. Thus the method used in the model is a PECE method. Ie. Predict Evaluate Correct Evaluate.