Again a really crude dynamic model for this. Let M be the distance South from the lake mouth to the Mfolozi mouth and F( t) be the flow in the Mfolozi. Under low and normal flow conditions the mouth progresses northwards, under extreme flood conditions it scours rapidly south wards. Geological controls bound the mouth north at the lake mouth and south at Maphelana, 1750m south of the lake mouth.
Thus the bounds give us f( M > Maphelana, whatever) < 0 and f( M < 0, whatever) > 0.
The progression must satisfy 
(so it takes about 5 years) and 
.
In an extreme event, the sand bar probably doesn't just scour neatly from the north, but would in fact ``overtop'' near Maphelana. However it is hard to cope with such discontinuities when using a higher order differential equation solver. In fact, as the data record does include such an extreme event, to prevent a wild response from the mouth model I have included a ``floodMax'' parameter. The effect is the same, even if the exact route is different, ie. the mouth scours back to Maphelana in very short order.
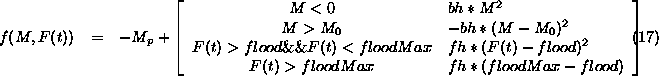
Where 
the distance
between from Maphelana to the lake mouth. 
is the definition of a flood and 
. 
is the normal rate of northward progress.
The bounds hardness bh = 1.1573e-5/m/sec, the flood hardness 
.
Figure 7 shows the 3D view of the function f(M,F).
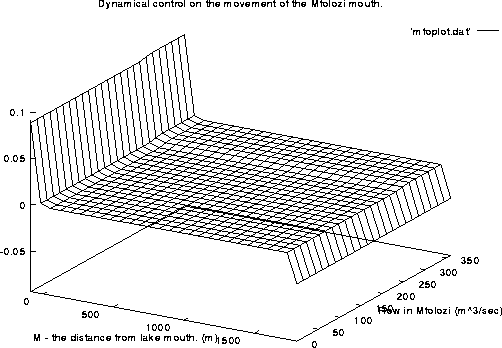
Figure 7: Dynamic control on the position of the Mfolozi mouth.